Understanding binary is one of the most important things in programming. Will teach you how to transform from decimal to binary and vice versa.
We all know that computers store data in binary.
In everyday life, starting from school we use the decimal system.
A number in the decimal system is decomposed like this:
125 = (1 * 10^2) + (2 * 10^1) + (5 * 10^0)
125 = 100 + 20 + 5Of course, we don’t need the brackets, but this way we make the calculation a little easier to follow.
In the above example, 1 is the first number in 125. It’s multiplied by 10 because this is the decimal system (base ten) at the power of 2, because this is the second number counting from the right. Keep in mind that we include 0 when we count.
This is why in the number 125, 5 is the 0 number, 2 is the first number and 1 is the second number. Sounds confusing? Unless you often skipped math classes in school, you should already know this .
Let’s consider a bigger number, 495763:
4 -> 5 (Fifth number)
9 -> 4 (Forth number)
5 -> 3 (Third number)
7 -> 2 (Second number)
6 -> 1 (First number)
3 -> 0 (Zero number)If we have a number like 125.983 it would be represented like this:
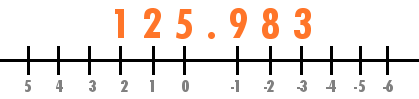
125.983 = 1 * 10^2 + 2 * 10^1 + 5 * 10^0 + 9 * 10^-1 + 8 * 10^-2 + 3 * 10^-3As you can see, the numbers after the ‘.’ (dot) are multiplied by ten at negative powers!
This means that in the number 125.983, 1 is the second number, 2 is the first number, 5 is the 0 number, 9 is the -1 number, 8 is the -2 number and 3 is the -3 number. That means that 0 is actually considered positive.
Probably the following graphic will make you understand easier:
Binary to decimal
Computers store data in binary. That is 0 and 1, false and true, off or on…
For example, in a circuit a 0 voltage could represent false, and the voltage 5V could represent true.
For the beginner it’s easier to learn to convert from binary to decimal first.
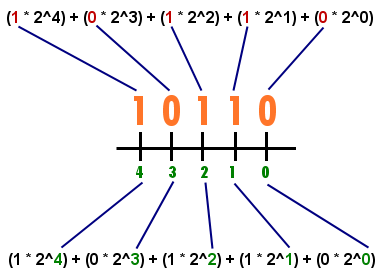
Suppose we have the binary number 10110:
10110 = (1 * 2^4) + (0 * 2^3) + (1 * 2^2) + (1 * 2^1) + (0 * 2^0) = 16 + 0 + 4 + 2 + 0 = 22It seems like the binary 10110 is the decimal number 22.
It’s time for some explanation.
Remember, decimal means base ten. That is why we multiplied the numbers by ten.
Binary means base two. This is why we multiply numbers by two.
Let’s take the first part:
(1 * 2^4)1 is the first number from ‘10110’. We multiply it by 2 (binary is base two) at the power of the number’s number (position). Confusing, heh? Remember from decimal and view the following graphic that I’m sure it will make you understand much better than I will by mumbling here.
Decimal to binary
A bit more difficult is to convert from decimal to binary.
Suppose we have the number 91 and we want to convert it to binary.
See the following graphic:
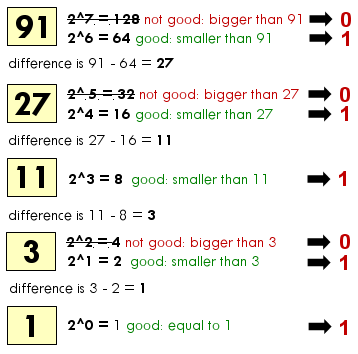
First we find the largest power of 2 that is less than 91. Because 2^7 (128) is bigger than 91 we can’t use it. This is why we add a 0 to our binary number.
2^6 is 64. It is the largest power of 2 that is less than 91. That is why we put a 1 next to the 0 in our binary number.
Now we substract the difference between the number 91 and 64, the result of the largest power of 2 less than 91. The result (91 – 64) gives us 27.
Now we want to find the largest power of 2 that is less than 27.
The next power, 5 gives us 2^5 = 32. It’s bigger than 27, that means we add a 0 to our binary number. Till now our number is 010.
Next power, 4 gives us 2^4 = 16. It’s smaller than 27, therefore we add a 1 to our binary number and make the substraction of 27 – 16 and get the difference. The result of 27 – 16 is 11.
Now we search for the largest power of 2 less than 11.
2^3 gives us 8. It is less than 11, therefore we add another 1 to our binary number and again, do the substraction: 11 – 8 = 3.
The largest power of 2 less than 3.
The last one we did was 2^3, now we do 2^2. 2^2 is 4, and 4 is bigger than 3, therefore we add a 0 to binary number.
Now we do 2^1, that is 2. 2 is smaller than 3. We add a 1 to the binary number and make the difference between 3 and 2. That is 1.
Finally, 2^0 equals 1. 1 is equal with our earlier result, 1. This means we add a 1 to our binary number . 🙂
In conclusion our binary number is 01011011. In binary system, the leading 0’s have no sense. They don’t affect the number.
As a result, 01011011 is equal to 1011011 and equal to 000000001011011. Although, you usually write 1011011.
The following table shows you the first ten numbers in decimal and binary:
Decimal -> Binary
0 -> 0000
1 -> 0001
2 -> 0010
3 -> 0011
4 -> 0100
5 -> 0101
6 -> 0110
7 -> 0111
8 -> 1000
9 -> 1001Try converting some numbers from binary to decimal and from decimal to binary. You can use the Windows Calculator to verify your results. First select ‘Scientific’ from the ‘View’ menu.



